Одним из наиболее широко применяемых индикаторов в техническом анализе является индекс относительной силы (RSI). Этот индикатор измеряет размер изменения цен, чтобы узнать является ли цена актива перекупленной или перепроданной.
RS = EMAn(Up) / EMAn(Down)RSI = 100 — 100/ (1+RS)На графике для удобной визуализаций полученная величина преобразуется под то, чтобы значения входили в диапазон от 0 до 100%. В результате мы получаем индекс относительной силы, динамику которого можно увидеть на графике индикатора.
В этой записи я расскажу несколько путей как рассчитать RSI с помощью Python.
Вычисление RSI используя только Pandas
В следующем куске кода, есть три функций которые могут быть использованы для расчета RSI, используя только Python и Pandas. Вы передаете в функцию DataFrame, номер периода на котором будет основываться RSI и если вы хотите использовать простую скользящую среднюю (SMA) или экспоненциальную скользящую среднюю (EMA). По умолчанию используется EMA.
import pandas
def rsi(df, periods = 14, ema = True):
"""
Возвращает pd.Series с индексом относительной силы.
"""
close_delta = df['close'].diff()
# Делаем две серий: одну для низких закрытий и одну для высоких закрытий
up = close_delta.clip(lower=0)
down = -1 * close_delta.clip(upper=0)
if ema == True:
# Использование экспоненциальной скользящей средней
ma_up = up.ewm(com = periods - 1, adjust=True, min_periods = periods).mean()
ma_down = down.ewm(com = periods - 1, adjust=True, min_periods = periods).mean()
else:
# Использование простой скользящей средней
ma_up = up.rolling(window = periods, adjust=False).mean()
ma_down = down.rolling(window = periods, adjust=False).mean()
rsi = ma_up / ma_down
rsi = 100 - (100/(1 + rsi))
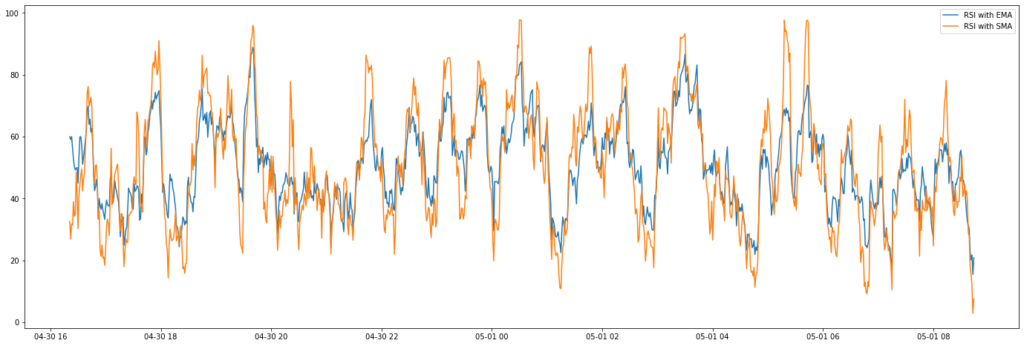
return rsiНиже представлена визуализация разницы чувствительности между рассчитанным RSI с использованием EMA и RSI рассчитанный с помощью варианта SMA.
На что стоит обратить внимание в использований метода ewm:
- Важно, чтобы вы использовали параметр min_periods в методе ewm, чтобы не рассчитывать RSI в первых периодах вашего временного ряда, который основан на неполных данных.
- Если вы устанавливаете параметр adjust в True, затухающий поправочный коэффициент будет использоваться в начале вашего временного ряда.
Расчет RSI используя обертку TA-lib Python
Если вы являетесь поклонником широко используемой библиотеки TA-lib, для вас есть хорошие новости. Расчет RSI поддерживается из коробки:
import talib as ta
ta.RSI(df['close'], timeperiod=14)TA-lib использует те же экспоненциальные скользящие средние, что описанные раннее в этом посте. Однако при первом расчете временного ряда, используется простая скользящая средняя. Вот почему он отличается вначале нашего временного ряда.
Расчет RSI используя библиотеку pandas-ta
Еще одним удобным пакетом для технического анализа в Python является pandas-ta. Пакет прост как TA-lib и использует версию EMA. Однако здесь тоже вначале временной серий, есть отличие от начальной функций представленной в этой статье. Это потому что он использует Wilder’s Moving Average.
import pandas_ta as pta
pta.rsi(df['close'], length = 14)Он поставляется с дополнительными параметрами. Такими как:
- scalar: умножение RSI на определенный скаляр — может вам нравится 1000 или 1?
- drift: вместо использования разницы цены закрытия в каждом периоде (drift = 1), вы можете использовать разницу цены закрытия в между периодами в течение более длительного периода времени.