В этой статье будет разобрано то как, вы можете оценивать линий поддержки и сопротивления для акций используя язык программирования Python.
Шаг1. Установка необходимых модулей
Первое, создайте файл и назовите его requirements.txt. Скопируйте в него следующее содержимое.
scipy==1.5.4
numpy==1.19.4
pandas==1.1.4
matplotlib==3.3.3
scikit-learn==0.23.2
pandas-datareader==0.9.0И запустите следующую команду в терминале.
pip install -r requirements.txtШаг1.1. Импорт необходимых модулей
import numpy as np
import pandas as pd
from math import sqrt
import matplotlib.pyplot as plt
import pandas_datareader as web
from scipy.signal import savgol_filter
from sklearn.linear_model import LinearRegressionПрименение подключаемых библиотек следующее:
- NumPy (Numeric Python, Числовой Python) — это библиотека для работы с многомерными массивами, включающая набор математических функций, которые применяются над операциями с этими массивами. За счет собственной оптимизации кода на языке C и Fortran обеспечиваются быстрые вычисления по сравнению с обычными структурами данных в Python.
- Pandas — это программная библиотека на языке Python для обработки и анализа данных.
- Модуль pyplot — это коллекция функций в стиле команд, которая позволяет использовать matplotlib почти так же, как MATLAB.
Шаг 2. Получение значение цены закрытия для акций
Здесь мы будем фокусироваться на акций AAPL в период с 1 января 2019 года по 1 апреля 2019, но вы можете применить тот же самый алгоритм к акциям в другой временной период. Для получения цены закрытия акций мы будем использовать pandas_datareader.
symbol = 'AAPL'
df = web.DataReader(symbol, 'yahoo', '2019-01-01', '2019-04-01')Результатом этого выражения будет объект pd.DataFrame с 6 столбцами. High, low, open, close, volume и adj close. Поскольку мы хотим увидеть только цены закрытия, мы можем сделать так.
series = df['Close']
series.index = np.arange(series.shape[0])В этих строчках кода, мы создаем объект pd.Series и сохраняем цены закрытия акций AAPL внутри переменной. Дальше мы устанавливаем индекс серий как массив последовательных чисел от 0 до количества цен закрытия которые мы имеем. Если вы напечатаете серию, вы получите следующее.
0 39.480000
1 35.547501
2 37.064999
3 36.982498
4 37.687500
...
57 46.697498
58 47.117500
59 47.180000
60 47.487499
61 47.810001
Name: Close, Length: 62, dtype: float64Вы можете построить серию и получить ее визуальное представление, используя matplotlib.
plt.title(symbol)
plt.xlabel('Days')
plt.ylabel('Prices')
plt.plot(series, label=symbol)
plt.legend()
plt.show()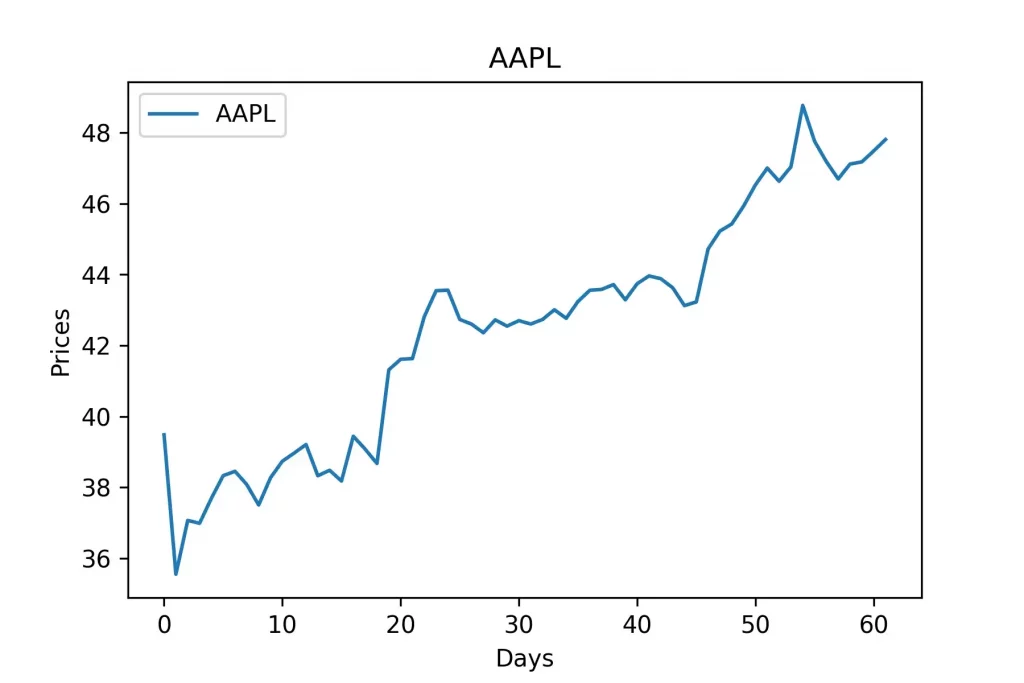
Пока наш код выглядит так.
import numpy as np
import pandas as pd
from math import sqrt
import matplotlib.pyplot as plt
import pandas_datareader as web
from scipy.signal import savgol_filter
from sklearn.linear_model import LinearRegression
symbol = 'AAPL'
df = web.DataReader(symbol, 'yahoo', '2019-01-01', '2019-04-01')
series = df['Close']
series.index = np.arange(series.shape[0])Шаг 3. Сглаживание графика
Сейчас данные на нашем графике не выглядят ровно и не подходят для анализа. На данном этапе мы попытаемся сгладить наш график используя функцию savgol_filter из модуля scipy.signal. Функция savgol_filter принимает 3 параметра. Ваш массив, длину окна и полипорядок. Ознакомиться к документаций этой функций можно по ссылке. Массив очевидно будет содержать серию наших данных. Вы можете думать о длине окна, как об уровне сглаживания которые вы хотите получить для своих данных. Чем больше длина окна, тем более гладким будет ваш график, и чем меньше длина окна, тем менее гладким будет ваш график. Чтобы определить длину окна, которую мы хотим использовать, я создал небольшой алгоритм, который покажу вам через минуту. Для этого проекта мы сохраним полипорядок, равный постоянному числу 3.
Шаг 3.1. Определение сглаживания
Чтобы определить желаемый уровень сглаживания, нам нужно найти количество имеющихся у нас данных за несколько месяцев. Поскольку в каждом месяце примерно 30 дней, мы разделим сумму цен, которые у нас есть на 30. Мы будем хранить эти данные в переменной month_diff. Если month_diff равно 0, то мы изменим значение на 1. Теперь, чтобы определить плавность графика, мы умножим наш month_diff на 2 и прибавим к нему 3.
month_diff = series.shape[0]
if month_diff == 0:
month_diff = 1
smooth = int(2 * month_diff + 3)
pts = savgol_filter(series, smooth, 3) Мы можем визуализировать это, используя matplotlib.
plt.title(symbol)
plt.xlabel('Days')
plt.ylabel('Prices')
plt.plot(pts, label=f'Smooth {symbol}')
plt.legend()
plt.show()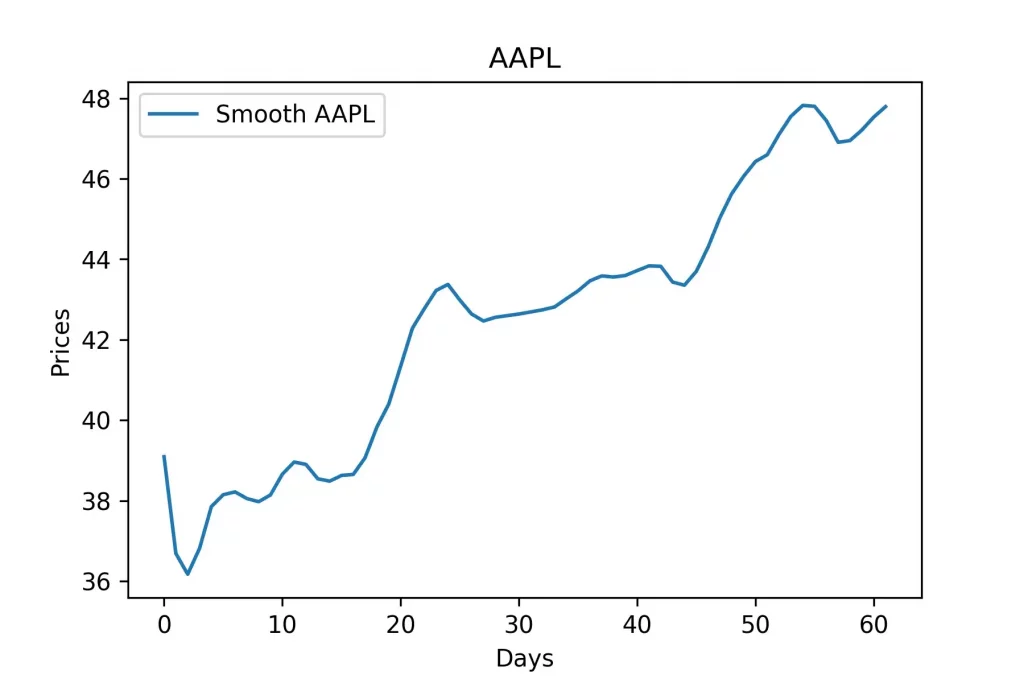
Мы можем визуализировать это в сравнений примерно так.
plt.title(symbol)
plt.xlabel('Days')
plt.ylabel('Prices')
plt.plot(series, label=symbol)
plt.plot(pts, label=f'Smooth {symbol}')
plt.legend()
plt.show()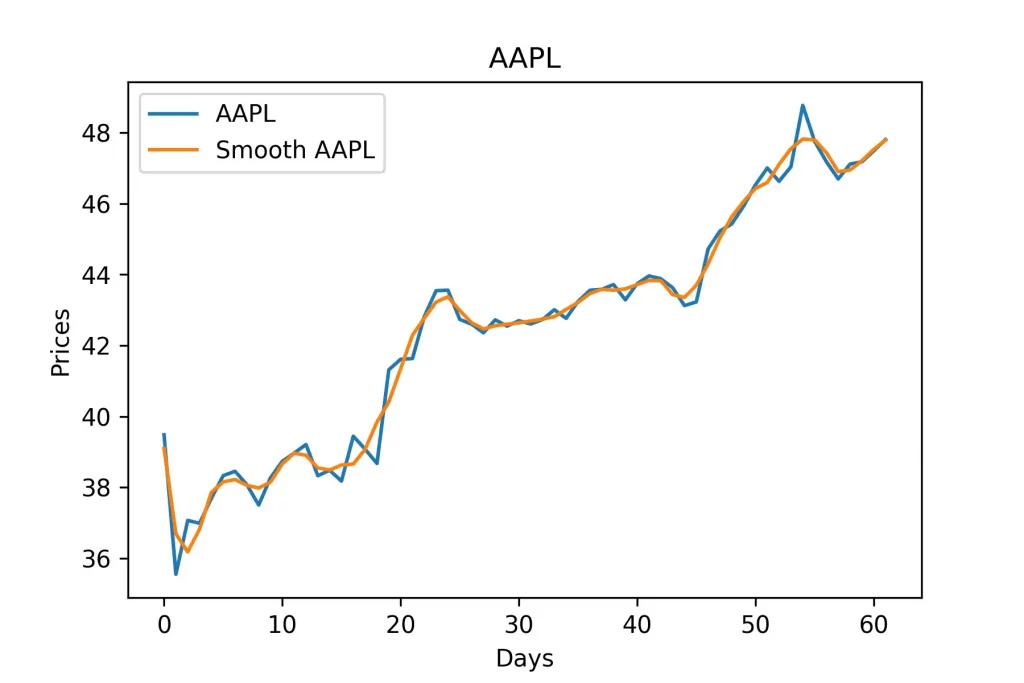
Шаг 4. Определение точек локального минимума и локального максимума
Для определения точек локального минимума и локального максимума написана следующая функция.
def pythag(pt1, pt2):
a_sq = (pt2[0] - pt1[0]) ** 2
b_sq = (pt2[1] - pt1[1]) ** 2
return sqrt(a_sq + b_sq)
def local_min_max(pts):
local_min = []
local_max = []
prev_pts = [(0, pts[0]), (1, pts[1])]
for i in range(1, len(pts) - 1):
append_to = ''
if pts[i-1] > pts[i] < pts[i+1]:
append_to = 'min'
elif pts[i-1] < pts[i] > pts[i+1]:
append_to = 'max'
if append_to:
if local_min or local_max:
prev_distance = pythag(prev_pts[0], prev_pts[1]) * 0.5
curr_distance = pythag(prev_pts[1], (i, pts[i]))
if curr_distance >= prev_distance:
prev_pts[0] = prev_pts[1]
prev_pts[1] = (i, pts[i])
if append_to == 'min':
local_min.append((i, pts[i]))
else:
local_max.append((i, pts[i]))
else:
prev_pts[0] = prev_pts[1]
prev_pts[1] = (i, pts[i])
if append_to == 'min':
local_min.append((i, pts[i]))
else:
local_max.append((i, pts[i]))
return local_min, local_maxПо существу, функция перебирает установленные точки с индексами от -1 до 1. Если точка меньше предыдущей и меньше точки впереди, то это локальный минимум. Аналогично, если точка больше чем предыдущая и больше чем точка впереди, то это локальный максимум.
Однако, если мы просто сделаем так, то алгоритм обнаружит множество локальных минимумов и максимумов. Поэтому используется теорема Пифагора для определения расстояния между предыдущей точкой и текущей точкой, а также расстояния между текущей точкой и следующей точкой. Тут продумано то, что считать точку локальным максимумом или минимумом только в том случае, если расстояние между ней и следующей точкой больше половины расстояния между ней и предыдущей точкой. Вот результат построения точек локального максимума и минимума.
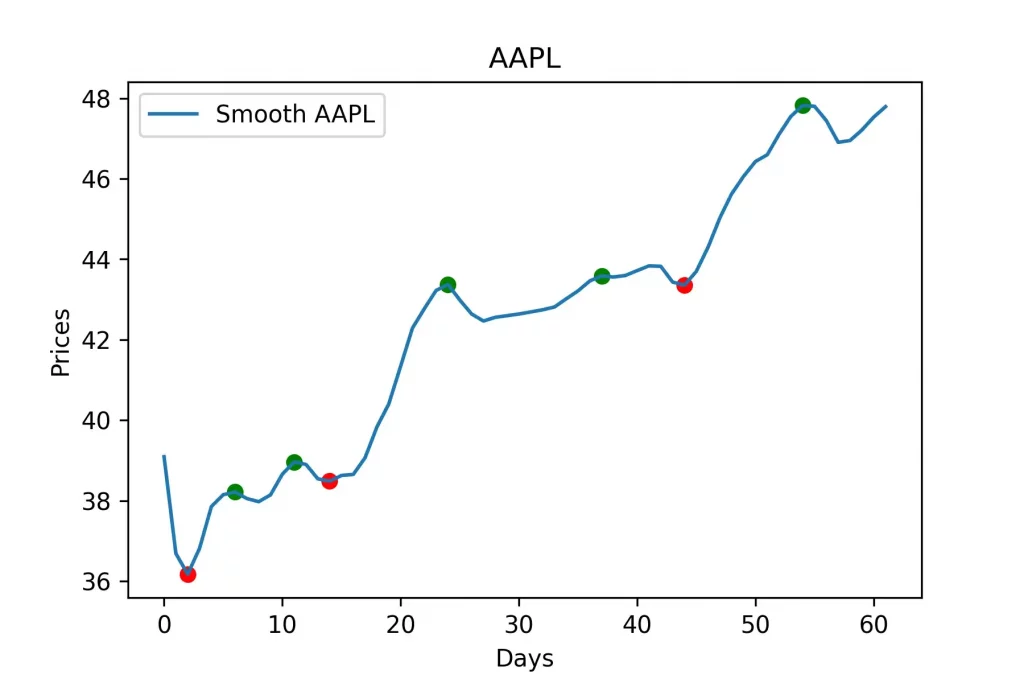
Шаг 5. Лучшая линия соответствия между локальным минимумом и локальным максимумом
Здесь мы собираемся найти две линии наилучшего соответствия. Один для локальных минимумов и один для локальных максимумов. Для этого мы будем использовать модель линейной регрессии. Как вы возможно уже знаете, уравнение для определения линий следующее y = mx + b, где m — наклон, а b — точка пересечения по оси y. Мы будем создавать функцию, которая будет возвращать наклон и точку пересечения по оси Y из набора точек.
def regression_ceof(pts):
return slope, y_int
local_min_slope, local_min_int = regression_ceof(local_min)
local_max_slope, local_max_int = regression_ceof(local_max)Сначала нам нужно получить точки x и y из pts, таким образом, сделав это мы получим понятный список. Помните, что pts — это список кортежей из точек.
[(x1, y1), (x2, y2), (x3, y3), (x4, y4), (x5, y5)]X = [pt[0] for pt in pts]
y = [pt[1] for pt in pts]
X = np.array(X)
y = np.array(y)
X = X.reshape(-1, 1)
X = np.array([pt[0] for pt in pts]).reshape(-1, 1)
y = np.array([pt[1] for pt in pts])Для этого нам просто нужно создать модель LinearRegression и подогнать наши данные X и Y.
def regression_ceof(pts):
X = np.array([pt[0] for pt in pts]).reshape(-1, 1)
y = np.array([pt[1] for pt in pts])
model = LinearRegression()
model.fit(X, y)
return model.coef_[0], model.intercept_
local_min_slope, local_min_int = regression_ceof(local_min)
local_max_slope, local_max_int = regression_ceof(local_max)Шаг 6. Создание линий поддержки и сопротивления
Создавать линии поддержки и сопротивления будет довольно просто. Мы будем использовать уравнение y = mx + b.
# y = (m * x) + b
support = (local_min_slope * np.array(series.index)) + local_min_int
resistance = (local_max_slope * np.array(series.index)) + local_max_intТеперь пришло время построить наши линии поддержки и сопротивления, и посмотреть насколько они точны. Вот так они выглядят на гладком графике.
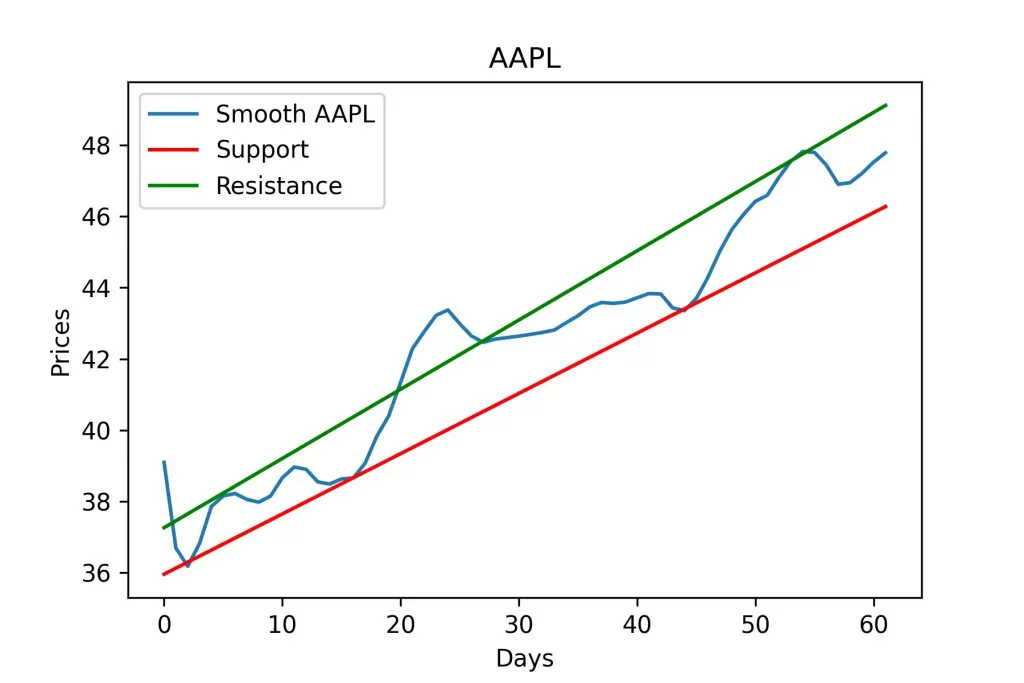
Вот так они выглядят на реальном графике.
plt.title(symbol)
plt.xlabel('Days')
plt.ylabel('Prices')
plt.plot(series, label=symbol)
plt.plot(support, label='Support', c='r')
plt.plot(resistance, label='Resistance', c='g')
plt.legend()
plt.show()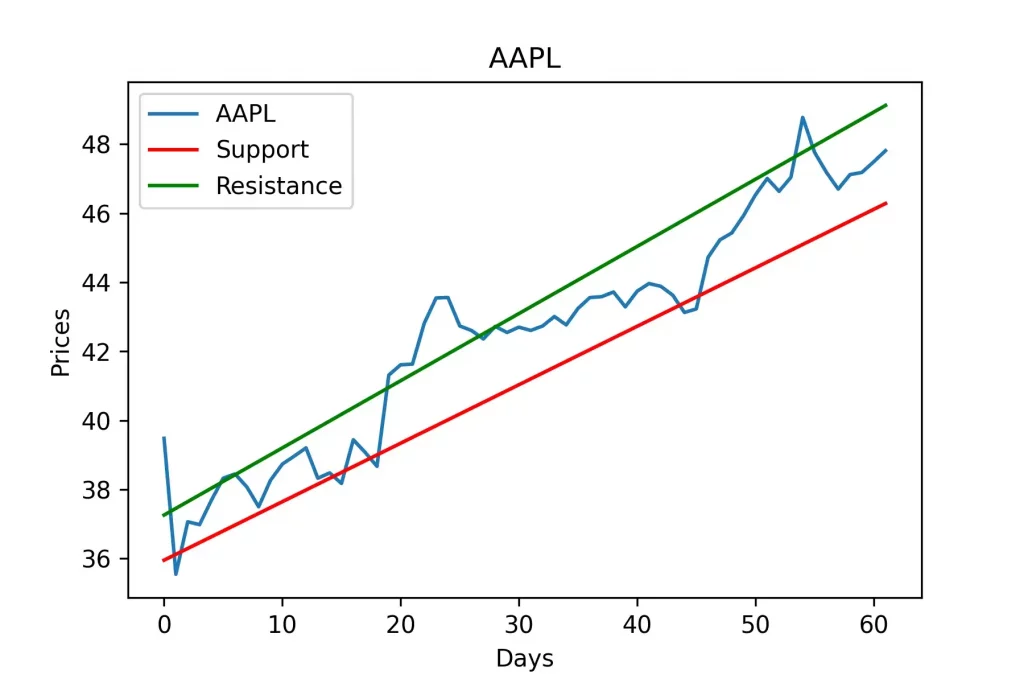
Он выглядит вполне точным.